Note
Go to the end to download the full example code
生成和提取旋转位移#
在本例中,我们将展示如何处理壳体和旋转位移。
并非所有单元类型都有旋转自由度,但一般来说,”壳” 单元都有。在本例中,我们创建一个厚度为 0.1 的正方形外壳,然后将其弯曲,产生旋转位移。
随后,我们绘制累积主应力图,并使用 ansys.mapdl.core.inline_functions.Query 提取正方形四个角的旋转位移精确值。
# start MAPDL and enter the pre-processing routine
from ansys.mapdl.core import launch_mapdl
mapdl = launch_mapdl()
mapdl.prep7()
*** MAPDL - ENGINEERING ANALYSIS SYSTEM RELEASE 2023 R1 23.1 ***
Ansys Mechanical Enterprise
20120530 VERSION=WINDOWS x64 22:04:48 JAN 26, 2024 CP= 0.750
***** MAPDL ANALYSIS DEFINITION (PREP7) *****
Mesh Setup#
在本例中,我们创建了一个简单的二维正方形,尺寸为 1 x 1,并赋予其 SHELL181 单元类型,因为该类型具有旋转自由度。接下来我们
给出该材料的弹性模量为 2e5 (EX)
将材料的主要泊松比定为 0.3 (PRXY)
将截面类型设置为 “SHELL”
将厚度设置为 0.1
将单元大小设置为 0.2
划分网格
绘制模型
mapdl.et(1, "SHELL181")
mapdl.mp("EX", 1, 2e5)
mapdl.mp("PRXY", 1, 0.3)
mapdl.rectng(0, 1, 0, 1)
mapdl.sectype(1, "SHELL")
mapdl.secdata(0.1)
mapdl.esize(0.2)
mapdl.amesh("all")
mapdl.eplot()

Applying Boundary Conditions#
进入求解层
将分析类型设为
STATIC。约束
x = 0节点的所有自由度在
x = 1处施加uz = -0.1的位移选择所有节点
求解模型
mapdl.run("/SOLU")
mapdl.antype("STATIC")
mapdl.nsel("s", "loc", "x", 0)
mapdl.d("all", "all")
mapdl.nsel("s", "loc", "x", 1)
mapdl.d("all", "uz", -0.1)
mapdl.allsel("all")
mapdl.solve()
*** NOTE *** CP = 0.812 TIME= 22:04:49
The automatic domain decomposition logic has selected the MESH domain
decomposition method with 2 processes per solution.
***** MAPDL SOLVE COMMAND *****
*** NOTE *** CP = 0.812 TIME= 22:04:49
There is no title defined for this analysis.
*** SELECTION OF ELEMENT TECHNOLOGIES FOR APPLICABLE ELEMENTS ***
---GIVE SUGGESTIONS ONLY---
ELEMENT TYPE 1 IS SHELL181. IT IS ASSOCIATED WITH ELASTOPLASTIC
MATERIALS ONLY. KEYOPT(8)=2 IS SUGGESTED AND KEYOPT(3)=2 IS SUGGESTED FOR
HIGHER ACCURACY OF MEMBRANE STRESSES; OTHERWISE, KEYOPT(3)=0 IS SUGGESTED.
*** MAPDL - ENGINEERING ANALYSIS SYSTEM RELEASE 2023 R1 23.1 ***
Ansys Mechanical Enterprise
20120530 VERSION=WINDOWS x64 22:04:49 JAN 26, 2024 CP= 0.812
S O L U T I O N O P T I O N S
PROBLEM DIMENSIONALITY. . . . . . . . . . . . .3-D
DEGREES OF FREEDOM. . . . . . UX UY UZ ROTX ROTY ROTZ
ANALYSIS TYPE . . . . . . . . . . . . . . . . .STATIC (STEADY-STATE)
GLOBALLY ASSEMBLED MATRIX . . . . . . . . . . .SYMMETRIC
*** NOTE *** CP = 0.812 TIME= 22:04:49
Present time 0 is less than or equal to the previous time. Time will
default to 1.
*** NOTE *** CP = 0.812 TIME= 22:04:49
The conditions for direct assembly have been met. No .emat or .erot
files will be produced.
D I S T R I B U T E D D O M A I N D E C O M P O S E R
...Number of elements: 25
...Number of nodes: 36
...Decompose to 2 CPU domains
...Element load balance ratio = 1.083
L O A D S T E P O P T I O N S
LOAD STEP NUMBER. . . . . . . . . . . . . . . . 1
TIME AT END OF THE LOAD STEP. . . . . . . . . . 1.0000
NUMBER OF SUBSTEPS. . . . . . . . . . . . . . . 1
STEP CHANGE BOUNDARY CONDITIONS . . . . . . . . NO
PRINT OUTPUT CONTROLS . . . . . . . . . . . . .NO PRINTOUT
DATABASE OUTPUT CONTROLS. . . . . . . . . . . .ALL DATA WRITTEN
FOR THE LAST SUBSTEP
SOLUTION MONITORING INFO IS WRITTEN TO FILE= file.mntr
*** NOTE *** CP = 0.828 TIME= 22:04:49
Predictor is ON by default for structural elements with rotational
degrees of freedom. Use the PRED,OFF command to turn the predictor
OFF if it adversely affects the convergence.
Range of element maximum matrix coefficients in global coordinates
Maximum = 7487.02512 at element 18.
Minimum = 7487.02512 at element 8.
*** ELEMENT MATRIX FORMULATION TIMES
TYPE NUMBER ENAME TOTAL CP AVE CP
1 25 SHELL181 0.000 0.000000
Time at end of element matrix formulation CP = 0.828125.
DISTRIBUTED SPARSE MATRIX DIRECT SOLVER.
Number of equations = 174, Maximum wavefront = 42
Process memory allocated for solver = 0.281 MB
Process memory required for in-core solution = 0.270 MB
Process memory required for out-of-core solution = 0.270 MB
Total memory allocated for solver = 0.518 MB
Total memory required for in-core solution = 0.497 MB
Total memory required for out-of-core solution = 0.497 MB
*** NOTE *** CP = 0.828 TIME= 22:04:49
The Distributed Sparse Matrix Solver is currently running in the
in-core memory mode. This memory mode uses the most amount of memory
in order to avoid using the hard drive as much as possible, which most
often results in the fastest solution time. This mode is recommended
if enough physical memory is present to accommodate all of the solver
data.
Distributed sparse solver maximum pivot= 29948.1005 at node 31 UX.
Distributed sparse solver minimum pivot= 0.248519178 at node 2 ROTZ.
Distributed sparse solver minimum pivot in absolute value= 0.248519178
at node 2 ROTZ.
*** ELEMENT RESULT CALCULATION TIMES
TYPE NUMBER ENAME TOTAL CP AVE CP
1 25 SHELL181 0.000 0.000000
*** NODAL LOAD CALCULATION TIMES
TYPE NUMBER ENAME TOTAL CP AVE CP
1 25 SHELL181 0.000 0.000000
*** LOAD STEP 1 SUBSTEP 1 COMPLETED. CUM ITER = 1
*** TIME = 1.00000 TIME INC = 1.00000 NEW TRIANG MATRIX
*** MAPDL BINARY FILE STATISTICS
BUFFER SIZE USED= 16384
0.062 MB WRITTEN ON ASSEMBLED MATRIX FILE: file0.full
0.312 MB WRITTEN ON RESULTS FILE: file0.rst
Plotting Stresses#
提取结果
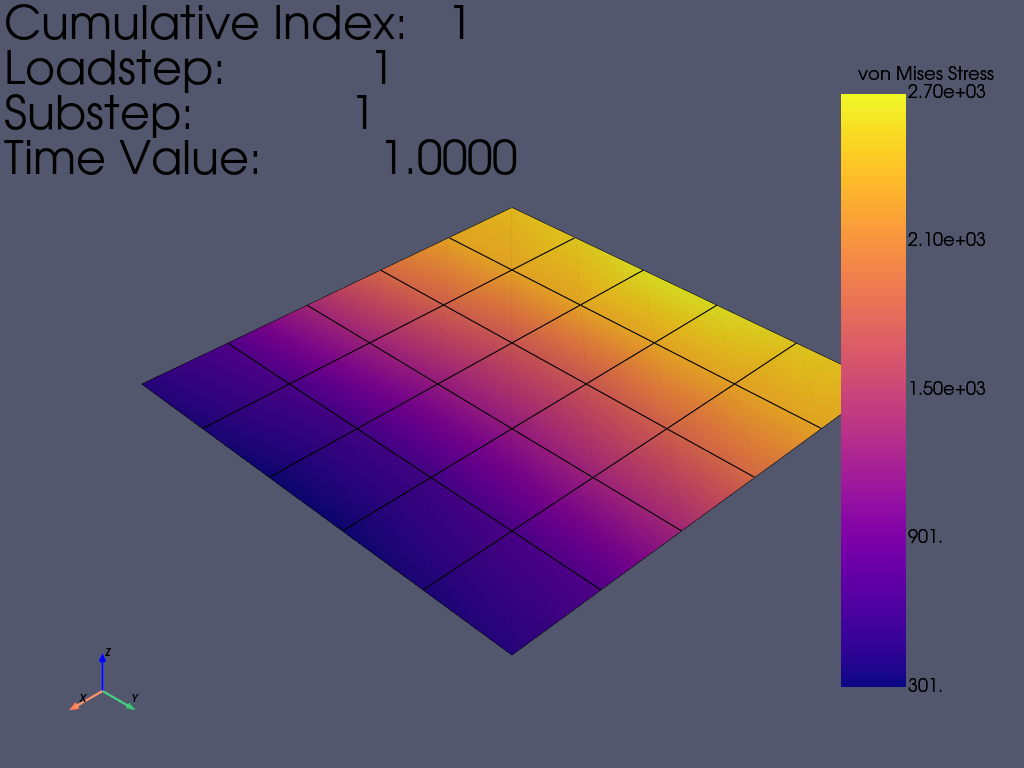
绘制累积 (0) 等效应力 (SEQV) 图
将 colormap 设置为 ‘plasma’,因为它在感知上是一致的
显示位移,以便我们看到任何变形
result = mapdl.result
result.plot_principal_nodal_stress(
0, "SEQV", show_edges=True, cmap="plasma", show_displacement=True
)
Extracting Rotational Displacements#
从
queries属性获取ansys.mapdl.core.inline_functions.Query实例在正方形的四个角上定位节点
分别提取所有 3 个旋转位移分量
全部打印出来
q = mapdl.queries
node1 = q.node(0, 0, 0)
node2 = q.node(0, 1, 0)
node3 = q.node(1, 0, 0)
node4 = q.node(1, 1, 0)
nodes = [node1, node2, node3, node4]
rotations = [(q.rotx(n), q.roty(n), q.rotz(n)) for n in nodes]
message = f"""
(0,1) B _________ C (1,1)
| |
| |
| |
|_________|
(0,0) A D (1,0)
N | (x_rot_disp, y_rot_disp, z_rot_disp)
--|------------------------------------
A | {rotations[0][0]:11.6f},{rotations[0][1]:11.6f},{rotations[0][2]:11.6f}
B | {rotations[1][0]:11.6f},{rotations[1][1]:11.6f},{rotations[1][2]:11.6f}
C | {rotations[2][0]:11.6f},{rotations[2][1]:11.6f},{rotations[2][2]:11.6f}
D | {rotations[3][0]:11.6f},{rotations[3][1]:11.6f},{rotations[3][2]:11.6f}
"""
print(message)
(0,1) B _________ C (1,1)
| |
| |
| |
|_________|
(0,0) A D (1,0)
N | (x_rot_disp, y_rot_disp, z_rot_disp)
--|------------------------------------
A | 0.000000, 0.000000, 0.000000
B | 0.000000, 0.000000, 0.000000
C | -0.000996, 0.155360, 0.000000
D | 0.000996, 0.155360, 0.000000
Stop mapdl#
mapdl.exit()
Total running time of the script: (0 minutes 1.320 seconds)