Note
Go to the end to download the full example code
建立有限元模型#
使用等参数公式为四边形单元建立了有限元模型,并用 PyMAPDL 进行了验证。
为了用一个具体的例子来说明,我们以一个二维单元为例,该单元由以下 (x, y) 节点位置、各向同性材料(杨氏模量为 30e6 psi,波依斯特比为 0.25)和单位厚度描述, 提供了 Daryl Logan 的《有限元法第一课》(第 2 版,PWS 出版社,1993 年)中讨论内容的实际应用。
import itertools
import matplotlib.pyplot as plt
import numpy as np
np.set_printoptions(linewidth=120) # 这些选项决定了浮点数、数组和其他 NumPy 对象的显示方式。
二维线性矩形单元刚度矩阵的推导#
用以下坐标建立一个基本的二维单元
node_xy = [(1, 2), (8, 0), (9, 4), (4, 5)]
node_ids = list(range(1, 1 + 4))
nodes = np.array(node_xy, dtype=float)
def plot_my_mesh(nodes, points=None):
fig = plt.figure(figsize=(6, 6))
ax = plt.gca()
plt.scatter(nodes[:, 0], nodes[:, 1])
if points is not None:
plot_pts = points if points.ndim > 1 else points[None, :]
plt.scatter(plot_pts[:, 0], plot_pts[:, 1])
nodes_around = np.reshape(np.take(nodes, range(10), mode="wrap"), (-1, 2))
plt.plot(nodes_around[:, 0], nodes_around[:, 1])
for i, n in enumerate(nodes):
ax.annotate(i + 1, n + np.array([0.1, 0.1]))
plt.xlim(0, 10)
plt.ylim(0, 6)
plt.box(False)
ax.set_aspect(1)
plt.show()
plot_my_mesh(nodes)
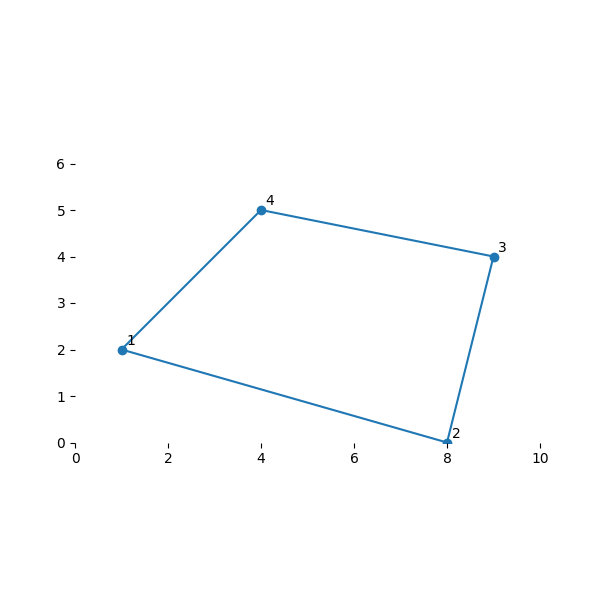
我们将创建一个单元类 MyElementDemo 来承载本演示所需的所有数据和方法。
虽然我们可以一次性对整个类进行编程(如本练习底部所做的),但我们将逐个添加数据和方法,以便对其含义进行注释。
我们将创建该类的一个实例,并将其称为 my_elem 以表示我们的特定单元示例
形函数#
通过单元形状函数,我们可以将某些量(例如位移分量)从角节点插值到整个单元的任意点。 这样,当结构发生变形时,我们不仅可以知道节点处的位移,还可以知道内部任意点的位移。
等参公式的特别之处在于为我们的二维单元选择一个典型形状。我们假设任何二维四边形都可以映射为正方形,例如 \({\rm I\!R}^2\) 中的一个域,如 \(s\in [-1,1]\) 和 \(t\in [-1,1]\)。 我们在该正方形上推导出所有物理量,并利用映射将它们的值转换为单元的实际形状。 这种变换将有助于简化计算所需的积分,以测量离散节点移动和形状变形时,应变能是如何在整个单元的连续体中累积的。
对于等参二维单元,我们定义了以下 4 个形状函数:
这些函数的构建方式是,节点 \(i\) 上的函数在所有其他节点上消失,并且它们的和在域中的所有点上都为 1。
为了好玩,让我们绘制一下它们,看看它们各自对单元的插值有什么贡献
s = np.linspace(-1, 1, 11)
t = np.linspace(-1, 1, 11)
S, T = np.meshgrid(s, t)
fig = plt.figure(figsize=(10, 10))
ax1 = fig.add_subplot(2, 2, 1, projection="3d")
ax1.plot_surface(S, T, 0.25 * (1 - S) * (1 - T))
ax1.title.set_text(r"N1")
ax2 = fig.add_subplot(2, 2, 2, projection="3d")
ax2.plot_surface(S, T, 0.25 * (1 + S) * (1 - T))
ax2.title.set_text(r"N2")
ax3 = fig.add_subplot(2, 2, 3, projection="3d")
ax3.plot_surface(S, T, 0.25 * (1 + S) * (1 + T))
ax3.title.set_text(r"N3")
ax4 = fig.add_subplot(2, 2, 4, projection="3d")
ax4.plot_surface(S, T, 0.25 * (1 - S) * (1 + T))
ax4.title.set_text(r"N4")
fig.tight_layout()
plt.show()
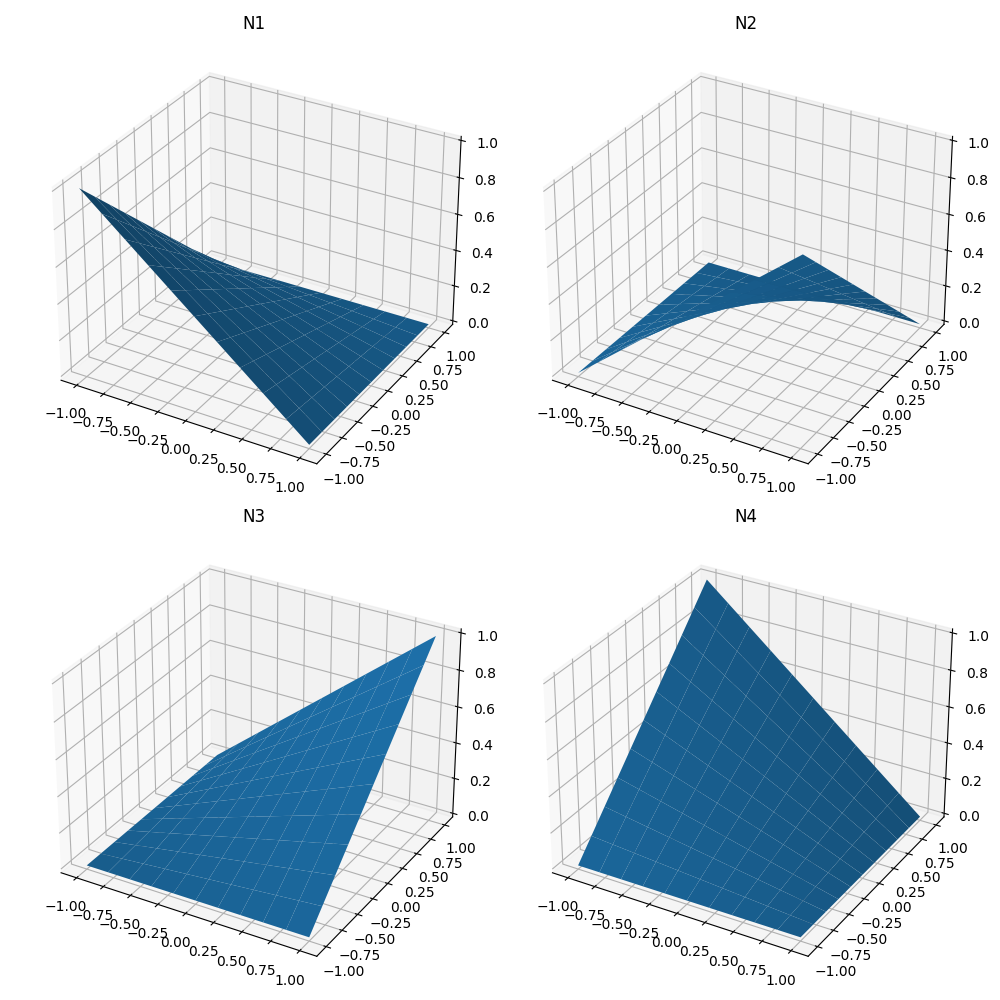
让我们将形状函数方法添加到我们的类中
要将一个量(如位置)从节点插值到整个单元中的任意点,我们可以使用以下操作。
为了了解这一点的用处,让我们来插值一些常见的点。 我们的等参单元的中心点为 \((s,t) = (0, 0)\) 。让我们看看插值是如何得到实单元中的等价点的:
array([5.5 , 2.75])
绘制网格
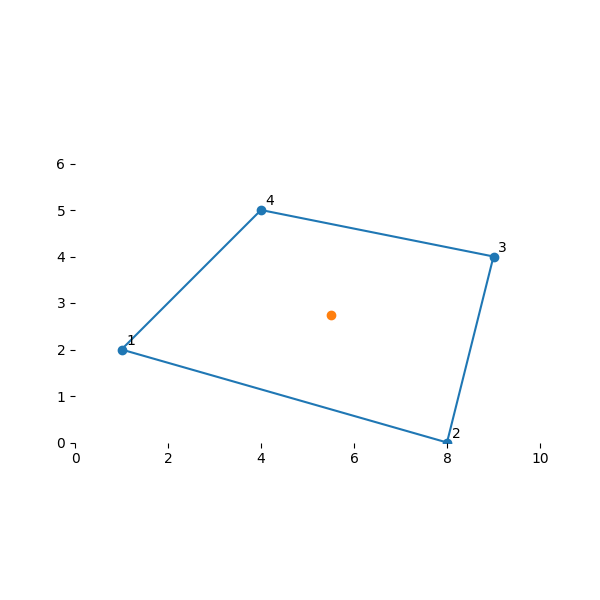
高斯积分#
高斯积分是一种用有限和 \(\sum w_i f(x_i)\) 近似函数 \(\int f(x) dx\) 的积分的方法。 通过在域中的有限位置对函数 \(f(x)\) 进行采样,并适当缩放其值,就可以得到积分的估计值。 事实证明,取样点 \(x_i\) 及其权重值 \(w_i\) 存在最佳位置。 对于我们的等参数单元域中的二维函数,即 \((s,t) \in {\rm I\!R}^2\) 且 \(s \in [-1,1]\) 和 \(t\in [-1,1]\), 4 个点积分的最佳位置是:
gauss_pts = (
np.array([[-1, -1], [1, -1], [1, 1], [-1, 1]], dtype=float) * 0.57735026918962
)
MyElementDemo.gauss_pts = gauss_pts
MyElementDemo.gauss_pts
array([[-0.57735027, -0.57735027],
[ 0.57735027, -0.57735027],
[ 0.57735027, 0.57735027],
[-0.57735027, 0.57735027]])
Their locations in the element of interest
gauss_pt_locs = np.stack(
[
my_elem.interpolate_nodal_values(*gauss_pt, nodes)
for gauss_pt in MyElementDemo.gauss_pts
]
)
plot_my_mesh(nodes, gauss_pt_locs)
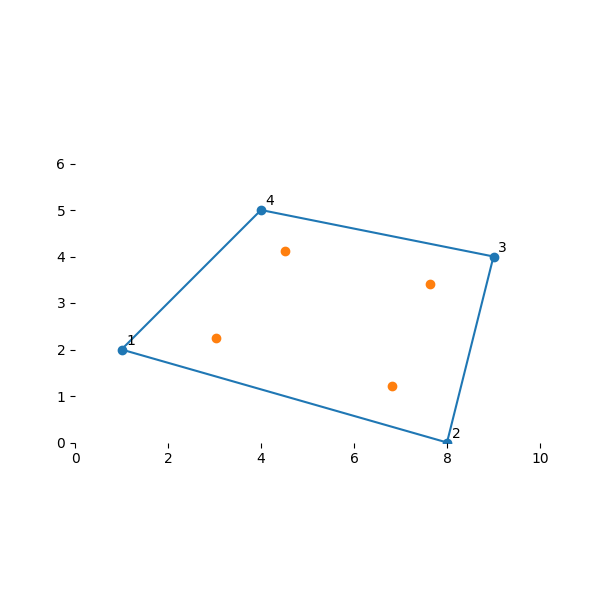
Strain calculation#
应变通过线性微分算子与位移相关。对于二维结构,我们只考虑其平面内分量:
并推断出微分算子如下
我们回顾一下,由于形函数,整个单元的位移 \(begin{bmatrix}u_x & u_y\end{bmatrix}^T\) 是已知的。 因此
为了将形函数纳入上述应变表达式,我们需要将相对于 \(x\) 和 \(y\) 的微分算子替换为以 \(s\) 和 \(t\) 表示的等价算子。 这就需要使用链式法则,而在多元微积分中,Jacobian 矩阵(及其行列式)为链式法则提供了便利:
因此:
其中
and
Implementation: Jacobians#
在形函数的帮助下,将位置 \(x\) 和 \(y\) 的表达式替换为节点位置的函数,就可以得到雅各比。结果相当于下面的双线性形式:
我们现在已经准备好在我们的单元中实施它了
接下来,我们将研究雅各布因子在单元内部是如何变化的。 First for our subject element:
my_elem.J(-1, -1), my_elem.J(0, 0), my_elem.J(1, 1)
(6.75, 6.0, 5.25)
Implementation: B Matrix#
Similarly, we can implement our expression for the B matrix, which converts nodal displacements \(\mathbf{u_{\text{nodal}}}\) to strains \(\mathbf{\varepsilon}\), by substituting the D operator, the shape functions and nodal locations:
where
and
for
def grad_N(self, s, t):
return 0.25 * np.array(
[
[-(1 - t), +(1 - t), +(1 + t), -(1 + t)],
[-(1 - s), -(1 + s), +(1 + s), +(1 - s)],
],
dtype=float,
)
def B(self, s, t):
j = self.J(s, t)
S = np.array([-1 + s, -1 - s, +1 + s, +1 - s], dtype=float)
T = np.array([-1 + t, +1 - t, +1 + t, -1 - t], dtype=float)
[d, c], [a, b] = (
0.25 * np.c_[self.nodes[:, 0], self.nodes[:, 1]].T.dot(np.c_[S, T])
).tolist()
n = self.grad_N(s, t)
def _bi_(i):
return np.array(
[
[a * n[0, i] - b * n[1, i], 0],
[0, c * n[1, i] - d * n[0, i]],
[c * n[1, i] - d * n[0, i], a * n[0, i] - b * n[1, i]],
],
dtype=float,
)
return 1.0 / j * np.c_[_bi_(0), _bi_(1), _bi_(2), _bi_(3)]
MyElementDemo.grad_N = grad_N
MyElementDemo.B = B
my_elem.B(0, 0)
array([[-0.10416667, 0. , 0.04166667, 0. , 0.10416667, 0. , -0.04166667, 0. ],
[ 0. , -0.08333333, 0. , -0.16666667, 0. , 0.08333333, 0. , 0.16666667],
[-0.08333333, -0.10416667, -0.16666667, 0.04166667, 0.08333333, 0.10416667, 0.16666667, -0.04166667]])
Stress Calculation#
The leap from strains to stresses involves the constitutive model, i.e., the material properties. This demo assumes a very simple case, i.e., a linear isotropic material which converts strains to stresses according to the following matrix:
class Isotropic:
def __init__(self, ex, nu):
self.nu = nu
self.ex = ex
def evaluate(self):
d = np.array(
[[1, self.nu, 0], [self.nu, 1, 0], [0, 0, (1 - self.nu) / 2.0]],
dtype=float,
)
return d * (self.ex / (1 - self.nu**2))
isotropic = Isotropic(30e6, 0.25)
Stiffness Calculation
The total energy of a system \(E\), comprising an element on which nodal forces \(\mathbf{F}_{\text{nodal}}\) are applied and undergoes nodal deformation \(\mathbf{u}_{\text{nodal}}\) is:
The first term stems from the work by the force at the nodes while the second measures the strain energy density accumulated throughout the element volume as it deforms.
As we saw, both stress and strain relate back to the nodal displacements through the B (courtesy of the shape functions), i.e., \(\mathbf{\varepsilon} = \mathbf{B} \cdot \mathbf{u}_{\text{nodal}}\) and \(\mathbf{\sigma} = \mathbf{C} \cdot \mathbf{B} \cdot \mathbf{u}_{\text{nodal}}\) thus:
Our assumed linear shape functions are not as rich as the true functions governing the actual deformation of the structure in real life. Imagine a Taylor expansion: our linear shape function captures up to the first polynomial term, whereas the true shape function could have arbitrarily many beyond that. One way this shows up is in the total energy of our system. When constrained to use our limited fidelity shape functions the system will accumulate a higher total energy than that of the true solution it is meant to approximate. To seek the best approximation, it makes sense to find a minimum of this total energy relative to the possible solutions, i.e., nodal displacements \(\mathbf{u}_{\text{nodal}}\). Loyal to our calculus roots, we look for the minimum by taking the corresponding partial derivative:
Thus, we’ve unlocked the Hooke’s law stiffness hidden in the integral:
For our planar element, assumed to have constant thickness \(h\) and area \(A\):
And the integral can be approximated by Gaussian quadrature through a weighted sum with the optimal sampling points for \(\mathbf{B}\):
Thus the use of an isoparametric formulation allowed us to make this integration easy, since the domain of integration is constant, regardless of the shape of the 2D quadrilateral at hand.
def K(self, C):
tot = np.zeros((self.ndof, self.ndof), dtype=float)
for st in self.gauss_pts:
B = self.B(*(st.tolist()))
J = self.J(*(st.tolist()))
tot += B.T.dot(C).dot(B) * J
return tot
MyElementDemo.K = K
MyElementDemo.ndof = 8
[[ 12875125.32026284 4266737.21733318 -1512012.17927291 2247558.57561918 -7065315.06442397 -4038004.53009543
-4297798.07656597 -2476291.26285693]
[ 4266737.21733318 12388604.21076075 4247558.57561918 6047863.05744317 -4038004.53009543 -3405127.91949808
-4476291.26285693 -15031339.34870584]
[ -1512012.17927291 4247558.57561918 11200772.34413869 -3259812.11243548 -3467825.1828747 -4443615.16468011
-6220934.98199108 3455868.70149641]
[ 2247558.57561918 6047863.05744316 -3259812.11243548 24720879.28409633 -2443615.16468011 -13747985.59281117
3455868.70149641 -17020756.74872833]
[ -7065315.06442397 -4038004.53009543 -3467825.1828747 -2443615.16468011 14535071.10764538 4332089.41368683
-4001930.86034672 2149530.28108871]
[ -4038004.53009543 -3405127.91949808 -4443615.16468011 -13747985.59281117 4332089.41368683 14955311.72255009
4149530.28108871 2197801.78975916]
[ -4297798.07656596 -4476291.26285693 -6220934.98199108 3455868.70149641 -4001930.86034672 4149530.28108871
14520663.91890376 -3129107.7197282 ]
[ -2476291.26285693 -15031339.34870584 3455868.70149641 -17020756.74872833 2149530.28108871 2197801.78975916
-3129107.7197282 29854294.307675 ]]
stiffness_scaled = np.round(stiffness / 1e4)
print(stiffness_scaled)
[[ 1288. 427. -151. 225. -707. -404. -430. -248.]
[ 427. 1239. 425. 605. -404. -341. -448. -1503.]
[ -151. 425. 1120. -326. -347. -444. -622. 346.]
[ 225. 605. -326. 2472. -244. -1375. 346. -1702.]
[ -707. -404. -347. -244. 1454. 433. -400. 215.]
[ -404. -341. -444. -1375. 433. 1496. 415. 220.]
[ -430. -448. -622. 346. -400. 415. 1452. -313.]
[ -248. -1503. 346. -1702. 215. 220. -313. 2985.]]
Putting it all together#
Creating Elem2D class.
class Elem2D:
gauss_pts = (
np.array([[-1, -1], [1, -1], [1, 1], [-1, 1]], dtype=float) * 0.57735026918962
)
nnodes = 4
ndof = 8
def __init__(self, nodes):
self.nodes = nodes
def B(self, s, t):
j = self.J(s, t)
S = np.array([-1 + s, -1 - s, +1 + s, +1 - s], dtype=float)
T = np.array([-1 + t, +1 - t, +1 + t, -1 - t], dtype=float)
[d, c], [a, b] = (
0.25 * np.c_[self.nodes[:, 0], self.nodes[:, 1]].T.dot(np.c_[S, T])
).tolist()
n = self.__grad_Ni(s, t)
def _bi_(i):
return np.array(
[
[a * n[0, i] - b * n[1, i], 0],
[0, c * n[1, i] - d * n[0, i]],
[c * n[1, i] - d * n[0, i], a * n[0, i] - b * n[1, i]],
],
dtype=float,
)
return 1.0 / j * np.c_[_bi_(0), _bi_(1), _bi_(2), _bi_(3)]
def __Ni(self, s, t):
return 0.25 * np.array(
[
(1 - s) * (1 - t),
(1 + s) * (1 - t),
(1 + s) * (1 + t),
(1 - s) * (1 + t),
],
dtype=float,
)
def __grad_Ni(self, s, t):
return 0.25 * np.array(
[
[-(1 - t), +(1 - t), +(1 + t), -(1 + t)],
[-(1 - s), -(1 + s), +(1 + s), +(1 - s)],
],
dtype=float,
)
def J(self, s, t):
upper = np.array(
[
[0, -t + 1, +t - s, +s - 1],
[0, 0, +s + 1, -s - t],
[0, 0, 0, +t + 1],
[0, 0, 0, 0],
],
dtype=float,
)
temp = upper - upper.T
return 1.0 / 8 * self.nodes[:, 0].dot(temp).dot(self.nodes[:, 1])
def k(self, C):
tot = np.zeros((self.ndof, self.ndof), dtype=float)
for st in self.gauss_pts:
B = self.B(*(st.tolist()))
J = self.J(*(st.tolist()))
tot += B.T.dot(C).dot(B) * J
return tot
def N(self, s, t):
n_vec = self.___Ni(s, t)
return np.array(
[
[n_vec[0], 0, n_vec[1], 0, n_vec[2], 0, n_vec[3], 0],
[0, n_vec[0], 0, n_vec[1], 0, n_vec[2], 0, n_vec[3]],
]
)
def M(self, rho):
tot = np.zeros((8, 8), dtype=float)
for st in self.gauss_pts:
n_array = self.N(*(st.tolist()))
tot += n_array.T.dot(n_array)
return tot
Isotropic class definition
class Isotropic:
def __init__(self, ex, nu):
self.nu = nu
self.ex = ex
def evaluate(self):
d = np.array(
[[1, self.nu, 0], [self.nu, 1, 0], [0, 0, (1 - self.nu) / 2.0]],
dtype=float,
)
return d * (self.ex / (1 - self.nu**2))
Applying the created classes.
isotropic = Isotropic(30e6, 0.25)
elem = Elem2D(nodes)
stiffness = elem.k(isotropic.evaluate())
stiffness_scaled = np.round(stiffness / 1e4)
print(stiffness_scaled)
[[ 1288. 427. -151. 225. -707. -404. -430. -248.]
[ 427. 1239. 425. 605. -404. -341. -448. -1503.]
[ -151. 425. 1120. -326. -347. -444. -622. 346.]
[ 225. 605. -326. 2472. -244. -1375. 346. -1702.]
[ -707. -404. -347. -244. 1454. 433. -400. 215.]
[ -404. -341. -444. -1375. 433. 1496. 415. 220.]
[ -430. -448. -622. 346. -400. 415. 1452. -313.]
[ -248. -1503. 346. -1702. 215. 220. -313. 2985.]]
Element in PyMAPDL#
Now let’s obtain the same stiffness matrix from MAPDL
launch PyMAPDL
from ansys.mapdl.core import launch_mapdl
mapdl = launch_mapdl()
mapdl.clear()
Create a use a 2-D 4-Node Structural Solid element with matching material properties.
mapdl.prep7()
mapdl.et(1, 182)
mapdl.mp("ex", 1, 30e6) # Young's modulus
mapdl.mp("nuxy", 1, 0.25) # Poisson's ratio
mapdl.mp("dens", 1, 1)
# unit density
MATERIAL 1 DENS = 1.000000
Create the nodes at the same locations as above.
Setup our element with the corresponding material properties.
Setup the static analysis.
mapdl.slashsolu()
mapdl.antype("static", "new")
PERFORM A STATIC ANALYSIS
THIS WILL BE A NEW ANALYSIS
Solve and permit one degree of freedom of each mode to be free per solution.
FINISH SOLUTION PROCESSING
*** NOTE *** CP = 0.000 TIME= 00:00:00
Distributed parallel processing has been reactivated.
***** ROUTINE COMPLETED ***** CP = 0.000
The columns of the stiffness matrix appear as nodal force reactions
[[12875000. 4266700.]
[-1512000. 2247600.]
[-7065300. -4038000.]
[-4297800. -2476300.]]
================================================================================
[[ 4266700. 12389000.]
[ 4247600. 6047900.]
[ -4038000. -3405100.]
[ -4476300. -15031000.]]
================================================================================
[[-1512000. 4247600.]
[11201000. -3259800.]
[-3467800. -4443600.]
[-6220900. 3455900.]]
================================================================================
[[ 2247600. 6047900.]
[ -3259800. 24721000.]
[ -2443600. -13748000.]
[ 3455900. -17021000.]]
================================================================================
[[-7065300. -4038000.]
[-3467800. -2443600.]
[14535000. 4332100.]
[-4001900. 2149500.]]
================================================================================
[[ -4038000. -3405100.]
[ -4443600. -13748000.]
[ 4332100. 14955000.]
[ 4149500. 2197800.]]
================================================================================
[[-4297800. -4476300.]
[-6220900. 3455900.]
[-4001900. 4149500.]
[14521000. -3129100.]]
================================================================================
[[ -2476300. -15031000.]
[ 3455900. -17021000.]
[ 2149500. 2197800.]
[ -3129100. 29854000.]]
================================================================================
Now, apply this to the whole matrix and output it.
stiffness_mapdl = np.array(results)
stiffness_mapdl = stiffness_mapdl.reshape(8, 8)
stiffnes_mapdl_scaled = np.round(stiffness_mapdl / 1e4)
print(stiffnes_mapdl_scaled)
[[ 1288. 427. -151. 225. -707. -404. -430. -248.]
[ 427. 1239. 425. 605. -404. -341. -448. -1503.]
[ -151. 425. 1120. -326. -347. -444. -622. 346.]
[ 225. 605. -326. 2472. -244. -1375. 346. -1702.]
[ -707. -404. -347. -244. 1454. 433. -400. 215.]
[ -404. -341. -444. -1375. 433. 1496. 415. 220.]
[ -430. -448. -622. 346. -400. 415. 1452. -313.]
[ -248. -1503. 346. -1702. 215. 220. -313. 2985.]]
Which is identical to the stiffness matrix obtained from our academic formulation.
print(stiffness_scaled)
[[ 1288. 427. -151. 225. -707. -404. -430. -248.]
[ 427. 1239. 425. 605. -404. -341. -448. -1503.]
[ -151. 425. 1120. -326. -347. -444. -622. 346.]
[ 225. 605. -326. 2472. -244. -1375. 346. -1702.]
[ -707. -404. -347. -244. 1454. 433. -400. 215.]
[ -404. -341. -444. -1375. 433. 1496. 415. 220.]
[ -430. -448. -622. 346. -400. 415. 1452. -313.]
[ -248. -1503. 346. -1702. 215. 220. -313. 2985.]]
Show that the stiffness matrix in MAPDL matches what we derived.
if np.allclose(stiffnes_mapdl_scaled, stiffness_scaled):
print("Both matrices are the equal within tolerance.")
Both matrices are the equal within tolerance.
Stop mapdl#
mapdl.exit()
Total running time of the script: (0 minutes 1.274 seconds)