2D 压力容器分析

本例演示如何创建一个基本压力容器并对其施加环向压力。

Objective

在本例中，我们将对管道进行内压应力分析。由于几何形状和负载的对称性，沿轴向的应变可以忽略不计，因此我们将此系统建模为二维平面应变。

Procedure

• 启动 MAPDL 实例

• 使用 PyMAPDL 将模型设置为 Python 函数

• 自动进行网格收敛研究

• 绘制感兴趣的结果

Additional Packages Used

• Matplotlib 用于绘图。

• NumPy 用于使用 NumPy 数组。

Problem Figure

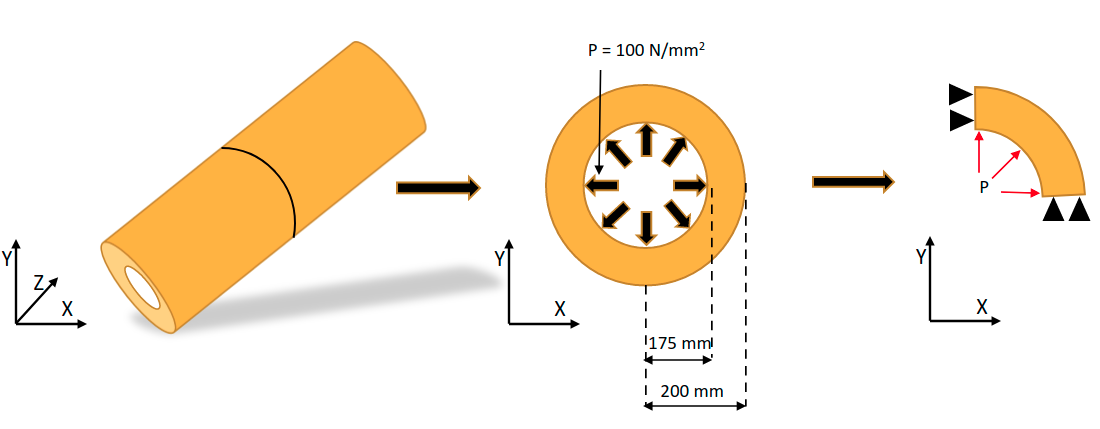
Launch MAPDL

import numpy as np
import matplotlib.pyplot as plt

from ansys.mapdl.core import launch_mapdl

# start mapdl
mapdl = launch_mapdl()

C:\Users\ff\AppData\Local\Programs\Python\Python310\lib\site-packages\ansys\tools\path\path.py:818: DeprecationWarning: This method is going to be deprecated in future versions. Please use 'get_mapdl_path'.
  warnings.warn(

使用 Python 函数设置管道横截面

我们在这里使用一个函数，这样就可以使用参数重建管道，而不用多次调用脚本。

def pipe_plane_strain(e, nu, inn_radius, out_radius, press, aesize):
    """Create 2D cross section modeling a pipe."""

    # 重置 mapdl
    mapdl.clear()
    mapdl.prep7()

    # 定义单元属性
    # Quad 4 node 182 with keyoption 3 = 2 (平面应变公式)
    mapdl.et(1, "PLANE182", kop3=2)

    # Create geometry
    # create a quadrant of the pressure vessel
    # We perform plane strain analysis on one quadrant (0deg - 90deg) of the
    # pressure vessel
    mapdl.pcirc(inn_radius, out_radius, theta1=0, theta2=90)
    mapdl.components["PIPE_PROFILE"] = "AREA" # 创建组件 “PIPE_PROFILE”，留一下这里的写法。 ————ff

    # Define material properties
    mapdl.mp("EX", 1, e)  # Youngs modulus
    mapdl.mp("PRXY", 1, nu)  # Poissons ratio

    # Define mesh controls
    mapdl.aesize("ALL", aesize)
    mapdl.mshape(0, "2D")  # mesh the area with 2D Quad elements
    mapdl.mshkey(1)  # free mesh
    mapdl.cmsel("S", "PIPE_PROFILE")  # Select the area component to be meshed
    mapdl.amesh("ALL")

    # 创建用于定义载荷和约束的组件
    mapdl.nsel("S", "LOC", "X", 0)  # 选择左上边缘的节点
    mapdl.components["X_FIXED"] = "NODES"  # 创建节点组件

    mapdl.nsel("S", "LOC", "Y", 0)  # 选择右下边缘的节点
    mapdl.components["Y_FIXED"] = "NODES"  # Create nodal component
    mapdl.allsel()

    mapdl.lsel("S", "RADIUS", vmin=rad1)  # 选择沿内径的线
    mapdl.components["PRESSURE_EDGE"] = "LINE"  # Create a line component
    mapdl.allsel()

    # Define solution controls
    mapdl.slashsolu()  # Enter solution
    mapdl.antype("STATIC", "NEW")  # Specify a new static analysis (Optional)

    mapdl.d("X_FIXED", "UX", 0)  # Fix the selected nodes in X direction
    mapdl.d("Y_FIXED", "UY", 0)  # Fix the selected nodes in Y direction

    # 将活动笛卡尔坐标系更改为圆柱坐标系
    mapdl.csys(1)

    # 对所选边缘施加均匀压力负荷
    mapdl.sfl("PRESSURE_EDGE", "PRES", press)

    # Solve the model
    mapdl.allsel()
    mapdl.solve()
    mapdl.finish()

    # Enter post-processor
    mapdl.post1()
    mapdl.set(1, 1)  # Select the first load step

    max_eqv_stress = np.max(mapdl.post_processing.nodal_eqv_stress()) # 获取节点处的等效应力值，并将其存储在 max_eqv_stress 变量中。
    all_dof = mapdl.mesh.nnum_all # 获取所有节点的编号（变量类型：数组），并将其存储在 all_dof 变量中。
    num_dof = all_dof.size # 获取所有节点的数量

    return num_dof, max_eqv_stress

Perform the mesh convergence study

# 定义模型输入参数
rad1 = 175  # Internal radius
rad2 = 200  # External radius
pressure = 100

e = 2e5  # Young's modulus
nu = 0.3  # Poisson's ratio

# 定义网格收敛参数
num_dof = []
max_stress = []

# 单元尺寸大小：使用 logspace，因为网格是按对数收敛的
esizes = np.logspace(1.4, 0, 20)

# 运行网格收敛并即时输出结果
for esize in esizes:
    dof, eqv_stress = pipe_plane_strain(e, nu, rad1, rad2, pressure, esize)
    num_dof.append(dof)
    max_stress.append(eqv_stress)
    print(f"DOF: {dof:5d}   Stress: {eqv_stress:.2f} MPa")

DOF:    28   Stress: 702.42 MPa
DOF:    48   Stress: 725.72 MPa
DOF:    57   Stress: 725.63 MPa
DOF:    66   Stress: 725.57 MPa
DOF:    78   Stress: 725.52 MPa
DOF:   124   Stress: 733.64 MPa
DOF:   144   Stress: 733.62 MPa
DOF:   215   Stress: 737.75 MPa
DOF:   250   Stress: 737.74 MPa
DOF:   354   Stress: 740.25 MPa
DOF:   490   Stress: 741.93 MPa
DOF:   656   Stress: 743.13 MPa
DOF:   873   Stress: 744.04 MPa
DOF:  1265   Stress: 745.32 MPa
DOF:  1632   Stress: 745.78 MPa
DOF:  2254   Stress: 746.50 MPa
DOF:  3230   Stress: 747.24 MPa
DOF:  4275   Stress: 747.60 MPa
DOF:  6141   Stress: 748.12 MPa
DOF:  8216   Stress: 748.40 MPa

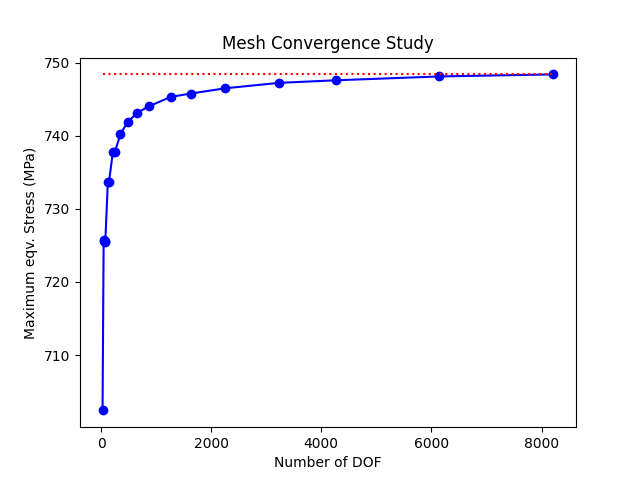
Plot mesh convergence results

画一条虚线表示收敛值

plt.plot(num_dof, max_stress, "b-o")
plt.plot([num_dof[0], num_dof[-1]], [max_stress[-1], max_stress[-1]], "r:")
plt.title("Mesh Convergence Study")
plt.xlabel("Number of DOF")
plt.ylabel("Maximum eqv. Stress (MPa)")
plt.show()

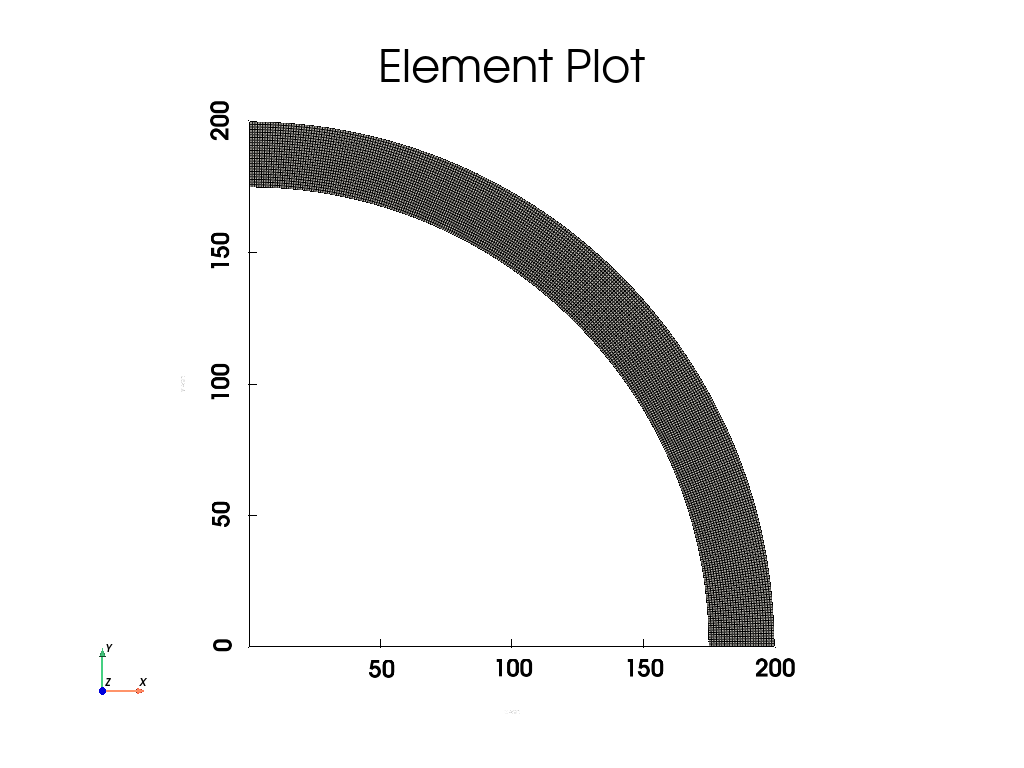
Resume results from last analysis from mesh convergence study

# 绘制最终的网格
mapdl.allsel("ALL")
mapdl.eplot(
    title="Element Plot",
    line_width=1,
    show_bounds=True,
    cpos="xy",
    background="w",
)

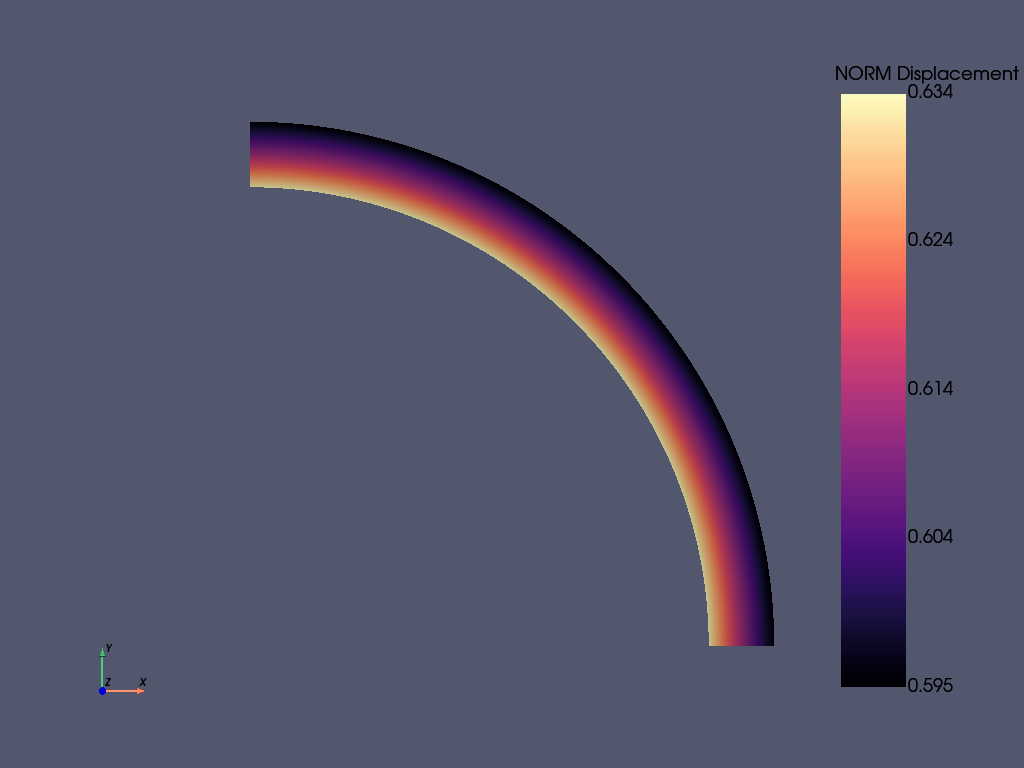
Plot nodal displacement

输入后处理 (/POST1) 并选择第一个荷载步

mapdl.post1()
mapdl.set(1, 1)

mapdl.post_processing.plot_nodal_displacement(
    component="NORM",
    cpos="xy",
    cmap="magma",
)

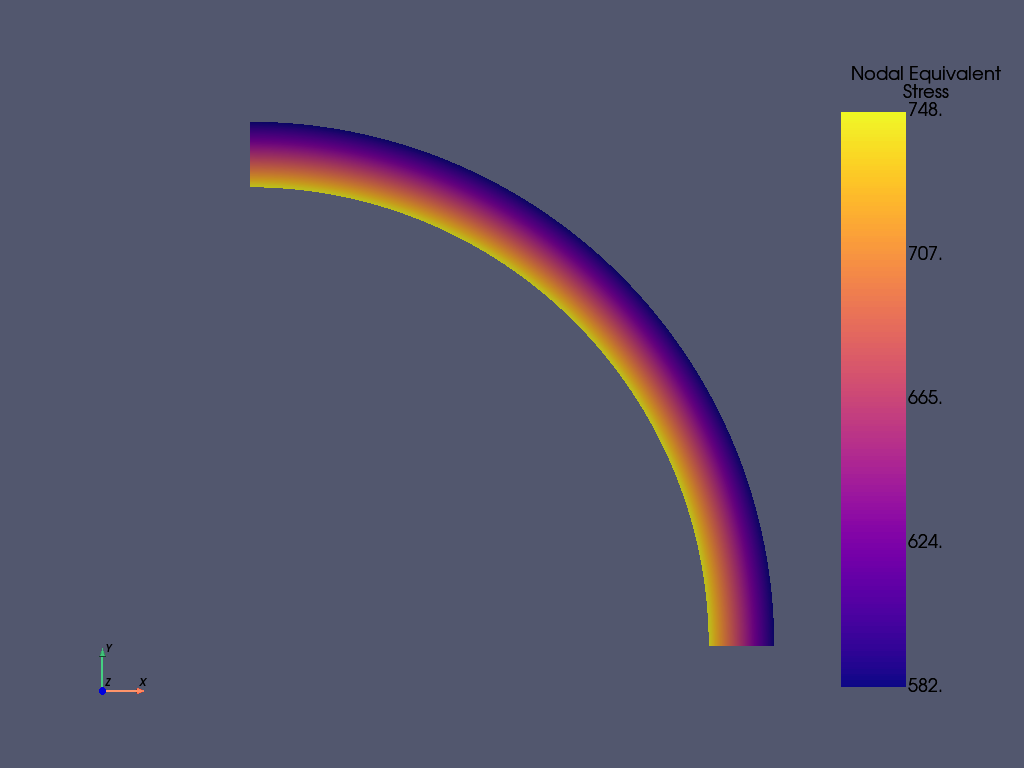
Plot nodal equivalent stress

mapdl.post_processing.plot_nodal_eqv_stress(cpos="xy", cmap="plasma")

Stop mapdl

mapdl.exit()